Interakce

Pružný - elastický rozptyl

Pružný rozptyl lze uvažovat ve dvou formách:

1.	Jednoduchý rozptyl jednotlivými atomy - částicová úvaha
	A.	Elektron interaguje s elektronovým obalem, výsledkem je malý úhel rozptylu
	B.	Elektron proniká elektronovým obalem a interaguje s jádrem, výsledkem je velký úhel rozptylu
		Obě tyto interakce by měly být nazývány téměř pružným rozptylem, protože ve skutečnosti dochází k jistým, poměrně malým ztrátám energie. Například interakce s jádrem vytváří brzdné rentgenové záření.
2.	Elektronová vlna interaguje s preparátem jako celkem - vlnová úvaha (difrakce)

Pružný rozptyl jednotlivými atomy

Celková pravděpodobnost výskytu srážky primárního elektronu
s elektronem v preparátu	s jádrem
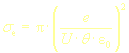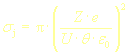Ze těchto vztahů je vidět, že rozptyl elektronem je funkcí energie primárního svazku a rozptyl jádrem> je navíc silně funkcí atomového čísla.

Pro rozptyl elektronů atomovým jádrem lze analogicky použít Rutherfordův diferenciální účinný průřez, který byl odvozen pro částice zpětně se odrážející od tenké kovové fólie. Základním předpokladem pro Rutherfordův rozptyl je, že elektron neztratí značnou energii během neelastických procesů, takže primární energie elektronu E je zachována. Stejně jako pro částice , čím menší je náměrná vzdálenost elektronu b od jádra, tím větší je úhel rozptylu.

Rozptyl elektronů na atomu:

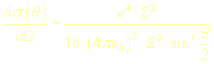
Integrací vztahu v příslušných mezích lze dospět ke vztahu pro výpočet účinného průřezu srážky elektronu s jádrem. Toto vyjádření počítá pouze s působením interaguje Coulombovské síly mezi jádrem a přibližujícím se elektronem, která způsobuje velký úhel rozptylu > 5°. Elektron pohybující se po dráze 1 na obrázku je odkloněn převážně interakcemi s elektronovým obalem. Elektrony pohybující se po drahách 2 a 3 začínají být na základě zmenšující se náměrné vzdálenosti stále více ovlivňovány jádrem, protože elektrony v obalu atomu nezastiňují elektrické pole jádra. Stínící efekt elektronového obalu je možno v následující rovnici zahrnout jako .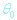

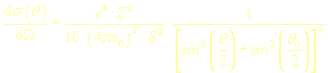
Stínící parametr 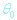je dán níže uvedenou rovnicí. Stínící efekt snižuje míru rozptylu. (úhel rozptylu bude menší) Pokud bude rozptylový úhel větší než 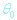, potom lze zanedbat interakce s elektronovým obalem a interakce s jádrem jsou dominantní. Hodnota 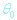při 100 keV je ~ 5° pro Cu a pro lehčí je prvky menší. Obecně je udáváno, že do 5° se jedná o rozptyl převážně elektronovým obalem a nad 5° se jedná o Rutherfordův rozptyl.

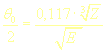
kde:

E

je energie primárního svazku v keV

Doposud se jednalo o nerelativistické účinné průřezy, Rutherfordovu rovnici se zohledněným stínícím efektem lze vyjádřit relativisticky pomocí kvantové mechaniky.

Problematika účinných průřezů je ještě mnohem složitější. Pro co nejreálnější simulace je Rutherfordův účinný průřez rozšiřován o hlediska, která také započítávají interakce přirozené vlny elektronu. Podstatné je, že na základě účinných průřezů vyplynuly souvislosti mezi úhlem a mechanismem rozptylu naznačené na obrázku.

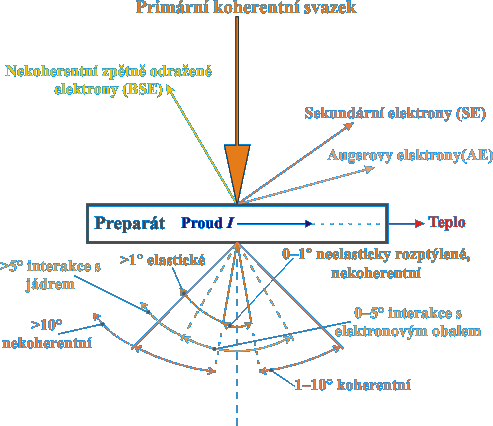
Úhlové rozdělení prošlých

elektronů:

Dále je patrna vazba mezi pravděpodobností srážky a energií primárního svazku, která velmi ovlivňuje interakci elektron-elektron a méně interakci elektron-jádro, kterou největší měrou řídí atomové číslo. Pro přípravu mikroskopických preparátů je také podstatná závislost interakce na tloušťce a hustotě.

Pružný kolektivní rozptyl - difrakce

Atomový rozptylový faktor popisuje rozptyl z vlnového hlediska a je doplňkový k Rutherfordovu srážkovému průřezu, protože se nejvíce uplatňuje při rozptylu v nízkých úhlech (do 5°), kde je Rutherfordův model nevhodný.

	je amplituda elektronové vlny rozptýlené na izolovaném atomu
	je rozptylová intenzita pro daný směr

Atomový rozptylový faktor je spojen s diferenciálním účinným průřezem tímto vztahem:

a je definován rovnicí:

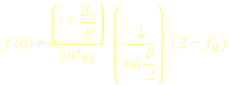
kde:	E0	je klidová energie elektronu
	E	je energie primárního svazku
	fX	je rozptylový faktor pro RTG (Rentgenovo) záření

Atomový rozptylový faktor obsahuje komponenty elastického rozptylu způsobeného jádrem v podobě atomového čísla a elastického rozptylu způsobeného elektronovým obalem v podobě rozptylového faktoru pro RTG záření.

Obrázek znázorňuje rovinnou vlnu tvořenou primárním svazkem elektronů, která postupuje naznačeným směrem a interaguje s rozptylovým centrem kolem kterého vzniká kulová rozptylová vlna. Tato vlna pak interferuje s původní rovinnou vlnou.

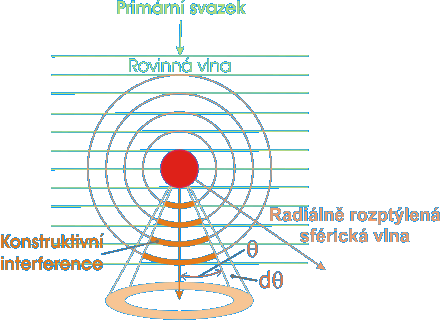
Interakce rovinné vlny

s rozptylovým centrem:

Primární elektronový svazek lze popsat následujícím vztahem jako rovinnou vlnu amplitudy 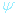a fáze kr, kde k je vlnový vektor (zde je k = 2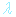^{. -1}, někdy v literatuře bývá udáván jako k = 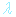^-1) a r je vzdálenost, kterou vlna urazí.

Potom pro rozptylovou sférickou vlnu 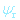platí dále uvedená rovnice, kde již vystupuje atomový rozptylový faktor jako atomová rozptylová amplituda závislá na směru (úhlu) rozptylu.

Popsaná rozptylová vlna a primární rovinná vlna spolu interferují. Pokud jsou ve fázi jde o konstruktivní interferenci a v určitých směrech vznikají difrakční vlny vyšších řádů, což je naznačeno na obrázku, kde primární svazek je nultého řádu.

Difrakce tvořená interferencí vln:

Difrakci lze zjednodušeně popsat Braggovým zákonem, přičemž uvažujeme, že se vlny chovají tak, jako by byly odráženy od atomových rovin, které reprezentují jednotlivé atomy.

kde d je meziatomární vzdálenost. Obrázek znázorňuje Braggův zákon graficky.

Braggův zákon:

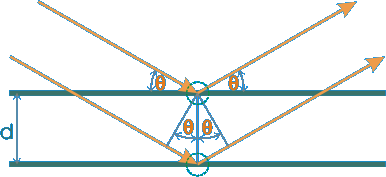
Difrakcí lze dobře krystalovou strukturu látky a také rozpoznávat prvky, z nichž je tvořena. Pokud elektronový svazek difraktuje s amorfně uspořádanými atomy, pak bude výsledná amplituda (intenzita) pro některé úhly výrazně vyšší, jak je naznačeno na obrázku.

Průběh amplitudy

amorfní látku:

Výsledný obraz zachycený na následujícím obrázku se bude pro amorfní látky jevit jako řada soustředných disků s plynulými přechody. Amorfní látky se vyznačují náhodným uspořádáním atomů, ale přesto mají jisté meziatomové mezery. Například lze relativně dobře definovat první a druhé nejbližší sousední mezery.

TEM difrakční snímek

amorfního uhlíku při 100 kV:

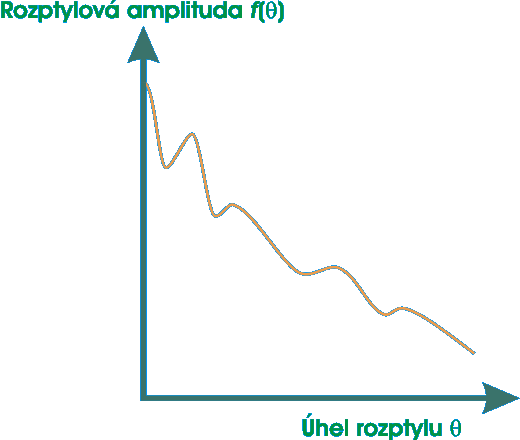
Difrakcí elektronového svazku s krystalickou látkou bude intenzita difrakčních paprsků maximální pro specifické úhly, které odpovídají Braggovu zákonu.

Průběh amplitudy pro

krystalickou látku:

Výsledný obraz pro polykrystalickou látku se bude jevit jako řada jasně ohraničených soustředných disků.

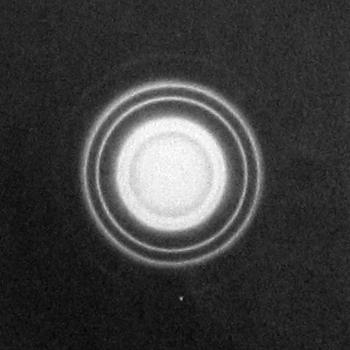
TEM difrakční snímek

polykrystalické zlato při 100 kV:

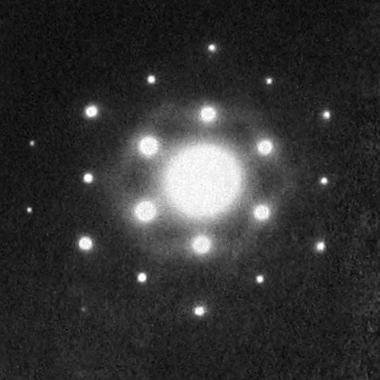
Látka tvořená z monokrystalu bude ve výsledném obrazu promítat opakující se krystalický motiv.

TEM difrakční snímek

monokrystal hliníku při 100 kV: