Interakce

Úvod

Aby mohl mikroskop zobrazit výsledný obraz, musí elektronový svazek interagovat s preparátem. Výsledkem interakce je nějaký ze signálů naznačených na obrázku, které nesou zobrazovanou informaci o mikrostruktuře. Obecně lze říct, že signály v horní části preparátu jsou užitečné především pro SEM a signály prošlých elektronů tvoří obraz v TEM.

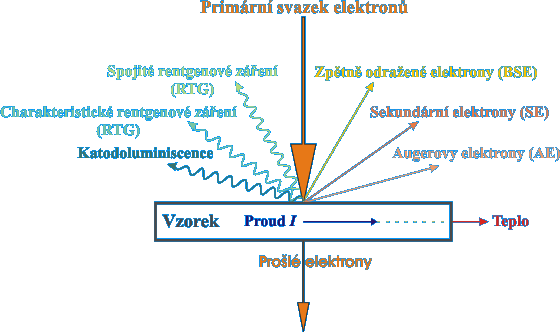
Možné interakce:

Elektronový rozptyl

Elektronový rozptyl lze dělit podle několika hledisek znázorněných na diagramu obrázku.

Rozdělení rozptylu:

Elasticita rozptylu závisí na tom, zda elektron při interakci ztratí svoji energii. Elektrony jsou koherentní v určitém rozsahu hodnot vlnové délky proto se mohou vyskytovat i elasticky rozptýlené nekoherentní elektrony. Směr rozptylu jako dopředný je brán rozptyl ve směru primárního elektronového svazku. Vícenásobný rozptyl je takový, jenž je tvořen více než jednou interakcí. V TEM je vícenásobný rozptyl nežádoucí, protože snižuje kvalitu obrazu – kontrast, jas.

Fyzikálně je rozptyl popisován pomocí účinného průřezu.

Účinný průřez - plocha

Účinný průřez vyjadřuje celkovou pravděpodobnost výskytu srážkové události s určitou částicí, vypočteme jej podle níže uvedeného vztahu, kde r je efektivní poloměr rozptylového centra, který nabývá určitou hodnotu pro každý rozptylový proces - elastický, neelastický. Pro představu ji lze chápat jako aktivní plochu částice v níž nastane srážka.

Totální účinný průřez je součtem elastického a neelastického účinného průřezu

Účinný průřez - tloušťka

Místo jedné částice je uvažován materiál v němž je N atomů.

kde:	A	je atomová hmotnost dané látky
	N0	je Avogadrova konstanta
		je hustota látky

Potom bude pro účinný totální průřez Q_T, který udává počet rozptylových událostí na jednotku vzdálenosti platit:

Má li vzorek tloušťku t, pak pravděpodobnost srážky p ve vzorku bude dána:

Součin se nazývá hmotnostní tloušťka. V tomto vztahu je vidět podstatná souvislost. Změna tloušťky nebo hustoty mají (každá z nich) stejný účinek na výslednou pravděpodobnost srážky. Tato souvislost je vidět i ze vzorce pro střední volnou dráhu .

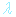Střední volná dráha udává průměrnou vzdálenost, kterou urazí elektron mezi dvěma srážkami a je určující pro tloušťku preparátu.

Účinný průřez - diferenciální

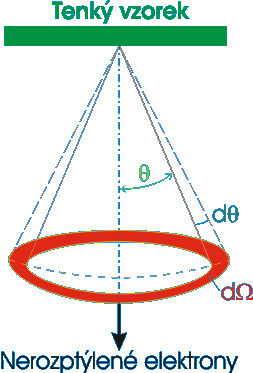
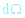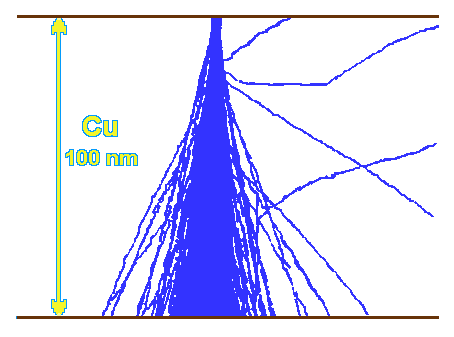
Diferenciální účinný průřez popisuje úhlové rozdělení rozptylu elektronů neboli pravděpodobnost, že elektron bude rozptýlen do prostorového úhlu . Lze jej nalézt v tabulkách a je hojně využíván pro počítačové simulace rozptylu elektronů pomocí metody Monte Carlo.

Elektrony jsou rozptylovány pod úhlem do prostorového úhlu , přírůstek 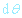odpovídá přírůstku prostorového úhlu 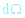, jak je patrno z obrázku.

Rozptyl elektronů do prostorového úhlu:

Mezi prostorovým úhlem a úhlem rozptylu platí geometrický vztah:

Derivací rovnice podle se získá diferenciál úhlu :

Úpravou rovnice dostáváme vztah pro diferenciální účinný průřez .

Integrací vztahu pro diferenciální účinný průřez lze vypočítat celkový účinný průřez. Meze integrálu se řídí faktem, že úhel rozptylu může nabývat hodnoty od 0 do radiánů.

Na obrázku jsou vykresleny trajektorie elektronů o energii 100 keV procházejících měděným terčíkem. Simulace je vytvořena pomocí metody Monte Carlo. Z výsledku je patrno, že se zvětšujícím úhlem rozptylu klesá hodnota výsledku účinného průřezu. Čím větší je úhel rozptylu, tím méně je do tohoto úhlu rozptýleno elektronů.

Trajektorie elektronů: